3 算例
![]()
![]() T
T ![]() [-500,500]
[-500,500]
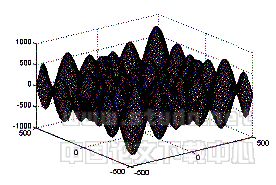
图1 函数f(x)特性示意图
函数f(x)有相当多的极小点,全局极小点是![]() =-420.97,
=-420.97,![]() =1,2,…,
=1,2,…,![]() ,最优值为-837.97;次最优点为
,最优值为-837.97;次最优点为![]() ={(
={(![]() ,
,![]() ,…,
,…,![]() ):
):![]() =-420.97,
=-420.97, ![]()
![]()
![]() ,
, ![]() =302.52},
=302.52},![]() =1,2,…,
=1,2,…,![]() ,次优值-719.53。变量个数n=2时函数f(x) 特性如图1示。程序编制和运行环境采用Fortran Power Station 4.0,随机数由内部随机函数产生,在奔腾133微机上运行。
,次优值-719.53。变量个数n=2时函数f(x) 特性如图1示。程序编制和运行环境采用Fortran Power Station 4.0,随机数由内部随机函数产生,在奔腾133微机上运行。
采用改进的Powell方法计算100次,初值在区间[-500,500]内随机产生,只有6次(即以概率0.06)搜索到全局最优,计算成功的概率极低。
Holland建立的标准(或简单)遗传算法,其特点是二进制编码、赌轮选择方法、随机配对、一点交叉、群体内允许有相同的个体存在。取种群规模m=30,交叉概率pc=0.95、变异概率pm=0.05,最大进化代数T=1000,每个变量用串长为L=16的二进制子串表示。二进制编码比浮点编码遗传算法计算精度低,对于标准遗传算法以目标函数小于-800为搜索成功,标准遗传算法运行100次。当取最大进化代数为T=200时,40次(以概率0.40)搜索到全局最优,平均计算时间为0.51秒;当取T=500时,51次(以概率0.51)搜索到全局最优,平均计算时间为1.13秒。
采用本文混合法计算,取m=30, pc=0.85、pm=0.2,T=100,进行Powell搜索的概率pPowell取不同值,混合法运行100次,计算结果见如表1。对于这个具有多极值的算例,多次计算表明pPowell=0.3时,混合法能以完全概率搜索到全局最优的准确值,但是此时混合法计算时间约为标准遗传算法取T=500时计算时间的4/5。对应的浮点编码遗传算法,取m=30,pc=0.85、pm=0.2,T=100,运行100次,82次(以概率0.82)搜索到全局最优(如表1中PPowell =0所示),计算时间约为标准遗传算法取T=500时计算时间的1/8,但是搜索到全局最优的概率却远远高于标准遗传算法。
表1 pPowell取不同值时混合法的计算结果
|
PPowell |
0.0 |
0.02 |
0.05 |
0.1 |
0.2 |
0.3 |
|
求得最优解的次数 |
82 |
85 |
89 |
94 |
98 |
100 |
|
求得最优解的概率 |
0.82 |
0.85 |
0.89 |
0.94 |
0.98 |
1.00 |
|
平均计算时间/ 秒 |
0.14 |
0.20 |
0.31 |
0.47 |
0.68 |
0.87 |
4 结束语
针对不可微函数的全局优化问题,本文提出一种把Powell方法与浮点编码遗传算法相结合的混合遗传算法,该算法兼顾了遗传算法全局优化方面的优势和Powell方法局部搜索能力较强的特点,提高求得全局解的概率。计算结果表明混合法优于遗传算法和Powell法,可以可靠地搜索到具有多个局部极值的函数优化问题的全局解。由于计算中只用到函数值信息,本文混合法不仅适用于不可微函数优化问题,也适合可微函数全局优化问题。
3 算例
![]()
![]() T
T ![]() [-500,500]
[-500,500]

图1 函数f(x)特性示意图
函数f(x)有相当多的极小点,全局极小点是![]() =-420.97,
=-420.97,![]() =1,2,…,
=1,2,…,![]() ,最优值为-837.97;次最优点为
,最优值为-837.97;次最优点为![]() ={(
={(![]() ,
,![]() ,…,
,…,![]() ):
):![]() =-420.97,
=-420.97, ![]()
![]()
![]() ,
, ![]() =302.52},
=302.52},![]() =1,2,…,
=1,2,…,![]() ,次优值-719.53。变量个数n=2时函数f(x) 特性如图1示。程序编制和运行环境采用Fortran Power Station 4.0,随机数由内部随机函数产生,在奔腾133微机上运行。
,次优值-719.53。变量个数n=2时函数f(x) 特性如图1示。程序编制和运行环境采用Fortran Power Station 4.0,随机数由内部随机函数产生,在奔腾133微机上运行。
采用改进的Powell方法计算100次,初值在区间[-500,500]内随机产生,只有6次(即以概率0.06)搜索到全局最优,计算成功的概率极低。
Holland建立的标准(或简单)遗传算法,其特点是二进制编码、赌轮选择方法、随机配对、一点交叉、群体内允许有相同的个体存在。取种群规模m=30,交叉概率pc=0.95、变异概率pm=0.05,最大进化代数T=1000,每个变量用串长为L=16的二进制子串表示。二进制编码比浮点编码遗传算法计算精度低,对于标准遗传算法以目标函数小于-800为搜索成功,标准遗传算法运行100次。当取最大进化代数为T=200时,40次(以概率0.40)搜索到全局最优,平均计算时间为0.51秒;当取T=500时,51次(以概率0.51)搜索到全局最优,平均计算时间为1.13秒。
采用本文混合法计算,取m=30, pc=0.85、pm=0.2,T=100,进行Powell搜索的概率pPowell取不同值,混合法运行100次,计算结果见如表1。对于这个具有多极值的算例,多次计算表明pPowell=0.3时,混合法能以完全概率搜索到全局最优的准确值,但是此时混合法计算时间约为标准遗传算法取T=500时计算时间的4/5。对应的浮点编码遗传算法,取m=30,pc=0.85、pm=0.2,T=100,运行100次,82次(以概率0.82)搜索到全局最优(如表1中PPowell =0所示),计算时间约为标准遗传算法取T=500时计算时间的1/8,但是搜索到全局最优的概率却远远高于标准遗传算法。
表1 pPowell取不同值时混合法的计算结果
|
PPowell |
0.0 |
0.02 |
0.05 |
0.1 |
0.2 |
0.3 |
|
求得最优解的次数 |
82 |
85 |
89 |
94 |
98 |
100 |
|
求得最优解的概率 |
0.82 |
0.85 |
0.89 |
0.94 |
0.98 |
1.00 |
|
平均计算时间/ 秒 |
0.14 |
0.20 |
0.31 |
0.47 |
0.68 |
0.87 |
4 结束语
针对不可微函数的全局优化问题,本文提出一种把Powell方法与浮点编码遗传算法相结合的混合遗传算法,该算法兼顾了遗传算法全局优化方面的优势和Powell方法局部搜索能力较强的特点,提高求得全局解的概率。计算结果表明混合法优于遗传算法和Powell法,可以可靠地搜索到具有多个局部极值的函数优化问题的全局解。由于计算中只用到函数值信息,本文混合法不仅适用于不可微函数优化问题,也适合可微函数全局优化问题。





